Best Description: Division Algorithm For Polynomials Proof. All answers, details & pictures are below.
Division Algorithm For Polynomials Proof
Division Algorithm for Polynomials states that given two polynomials, a dividend polynomial, and a nonzero divisor polynomial, there is a unique quotient polynomial and a unique remainder polynomial. Here, are the Division Algorithm For Polynomials Proof.
Let’s denote the divisor polynomial as P(x) and the divisor polynomial as D(x), where D(x) is nonzero. We want to find a quotient polynomial Q(x) and a remainder polynomial R(x), like this:
- P(x) = D(x) * Q(x) + R(x)
We can use polynomial long division to show the existence of quotient and remaining polynomials.
- Take the highest order term of the dividing polynomial P(x) and the highest order term of the dividing polynomial D(x). Divide the highest order P(x) term by the highest order D(x) term to obtain the leading term of the quotient polynomial Q(x).
- Multiply the divisor polynomial D(x) by the leading term of the quotient polynomial Q(x) to get a temporary polynomial T(x).
- Subtract T(x) from P(x) to get a new polynomial P1(x). P1(x) is obtained by subtracting the terms of T(x) from the corresponding terms of P(x).
- Repeat steps 1-3 with the new polynomial P1(x) as the numerator until the degree of P1(x) is less than the degree of D(x).
- The final polynomial obtained when the degree of P1(x) is less than the order of D(x), is the remaining polynomial R(x).
- The quotient polynomial Q(x) is the sum of all the quotient terms obtained in step 1 at each stage of the division. / Division Algorithm For Polynomials Proof
By performing the polynomial long division, we can get the quotient polynomial Q(x) and the remainder polynomial R(x). Therefore, we have demonstrated the existence of Q(x) and R(x).
- Uniqueness:
To prove the uniqueness of the quotient and remainder polynomials, we assume that there are two sets of quotients and remainder polynomials Q1(x), R1(x) and Q2(x), R2(x) and satisfy the following:
- P(x) = D(x) * Q1(x) + R1(x)
- P(x) = D(x) * Q2(x) + R2(x)
- Subtracting these two equations we get:
- D(x) * (Q1(x) – Q2(x)) = R2(x) – R1(x)
Since the degree of D(x) is not zero, the degree of the left side is at least the degree of D(x). But the degree of the right side is less than the degree of R2(x) – R1(x), D(x), because R2(x) and R1(x) are the remainders from polynomial long division.
This contradiction implies that the only probability is that the polynomials on both sides of the equation are equally zero. Therefore, we have:
- Q1(x) – Q2(x) = 0 and R2(x) – R1(x) = 0
Hence, Q1(x) = Q2(x) and R1(x) = R2(x), which proves the uniqueness of the quotient and remainder polynomials.
We proved the Division Algorithm for polynomials by demonstrating both the existence and uniqueness of quotient and remainder polynomials.
Division Algorithm For Polynomials Proof: This article concludes our article on polynomial division with several tasks. There is also a solution for every task. Additionally, you will find a detailed video with polynomial division tasks.
Polynomial division problem 1
- Calculate the polynomial part below
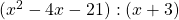
Solution to task 1
The term with the highest exponent in the first polynomial is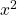 
. 
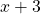To get a with the polynomial 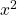, we need to 
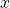multiply it by , i.e.
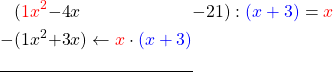
Division Algorithm For Polynomials Proof: We add to x^2the next term -4xand subtract the result of the previous multiplication from it.
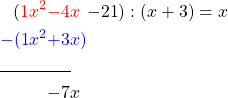
To -7x we add the next part of the first polynomial -21 and get.
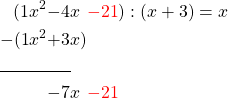
The term with the highest exponent is now –7x. We therefore need to multiply the second polynomial by –7, i.e .
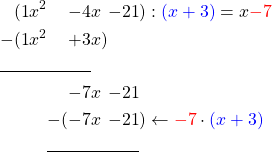
Now we subtract again.
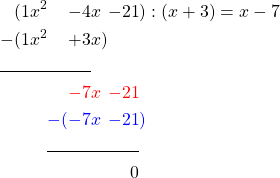
This brings us to the end of polynomial division.
Polynomial division problem 2
Calculate the following polynomial division.
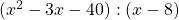
Solution to task 2
The term with the highest exponent in the first polynomial is x^2. x – 8 To make this vanish with the second polynomial , we need to xmultiply the second polynomial by , i.e.
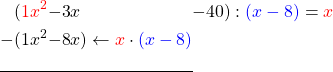
We add to x^2the next term -3xand subtract the result of the previous multiplication from it.
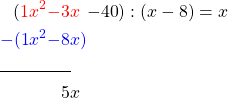
To 5x we add the next part of the first polynomial –40 and get.
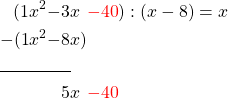
The term with the highest exponent is now 5x. We therefore need to multiply the second polynomial by 5, i.e.
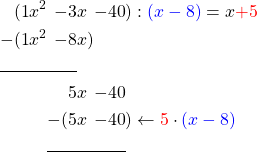
Now we subtract again.
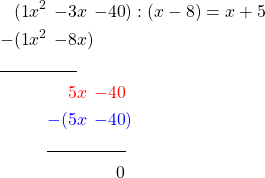
How do you verify the division algorithm for polynomials?
In polynomial division, the degree of the divisor is greater than or equal to the divisor. Multiply the divisor polynomial and the quotient, add to the remainder, if any, to verify the result.
Division Algorithm For Polynomials Proof video are below.
This brings us to the end of polynomial division. https://studyflix.de/mathematik/polynomdivision-aufgaben-2430 Division Algorithm For Polynomials Proof topic is over.
