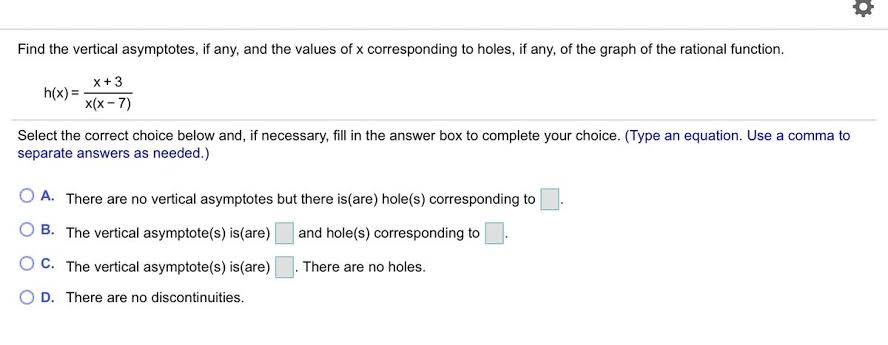
Find the vertical asymptotes, if any, and the values of x corresponding to holes: Best answer & explanation are below. Here, are the detailed description.
Find the vertical asymptotes, if any, and the values of x corresponding to holes
Find the vertical asymptotes, if any, and the value of x corresponding to holes, if any, of the graph of the following rational function. f(x) =x-3 / x²-9 ….. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (Type an integer or a fraction. Use a comma to separate answers as needed.)
- A. There are no vertical asymptotes but there is (are) hole(s) corresponding to x =
- B. Vertical asymptote(s) at x= There are no holes.
- C. Vertical asymptote(s) at x= and hole(s) corresponding to x =
- D. There are no discontinuities.
Final answer: The vertical asymptote of the given rational function is x=-3 and there is a hole at x=3.
Best Explanation:
To find the vertical asymptotes and the value of x corresponding to holes, we need to factor the numerator and denominator of the rational function.
- Given function: f(x) = (x-3) / (x²-9)
- Factoring the numerator: x-3
- Factoring the denominator: (x+3)(x-3)
- The denominator has a factor of (x-3), which means there is a hole at x=3.
- The denominator also has a factor of (x+3), which means there is a vertical asymptote at x=-3.
- Therefore, the correct choice is C. Vertical asymptote(s) at x=-3 and hole(s) corresponding to x=3.
Find the vertical asymptotes, if any, and the values of x corresponding to holes – video are below:

